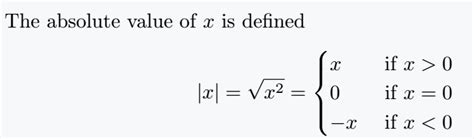Mastering Piecewise Defined Functions In Latex

Quick Links :

The world of mathematics is full of complexities and nuances, and one of the most important concepts in mathematics is the piecewise defined function. A piecewise defined function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. These functions are used to model real-world phenomena, such as the behavior of electrical circuits, the motion of objects, and the growth of populations.

What are Piecewise Defined Functions?

A piecewise defined function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. The function is defined as:

f(x) = { f1(x) if x ∈ I1 f2(x) if x ∈ I2 ... fn(x) if x ∈ In }

where I1, I2,..., In are disjoint intervals that cover the entire domain of the function.

Types of Piecewise Defined Functions

There are several types of piecewise defined functions, including:

• Continuous piecewise functions: These functions are continuous at every point in the domain.
• Discontinuous piecewise functions: These functions are discontinuous at one or more points in the domain.
• Piecewise linear functions: These functions are defined by linear sub-functions.
• Piecewise quadratic functions: These functions are defined by quadratic sub-functions.

How to Write Piecewise Defined Functions in LaTeX

LaTeX is a typesetting system that is widely used in mathematics and science. It is used to create professional-looking documents that contain mathematical equations and formulas. Writing piecewise defined functions in LaTeX is straightforward.

The basic syntax for writing a piecewise defined function in LaTeX is:

\begin{cases}
  f1(x) & \text{if } x \in I1 \\
  f2(x) & \text{if } x \in I2 \\
 ...
  fn(x) & \text{if } x \in In
\end{cases}

For example, the piecewise defined function:

f(x) = { x^2 if x < 0 x^3 if x ≥ 0 }

can be written in LaTeX as:

\begin{cases}
  x^2 & \text{if } x < 0 \\
  x^3 & \text{if } x \geq 0
\end{cases}

Common Pitfalls When Writing Piecewise Defined Functions in LaTeX

There are several common pitfalls to avoid when writing piecewise defined functions in LaTeX. These include:

• Forgetting to use the cases environment.
• Forgetting to use the & symbol to separate the function from the condition.
• Using the wrong symbol for the condition (e.g., using < instead of ≤).

Best Practices for Writing Piecewise Defined Functions in LaTeX

There are several best practices to follow when writing piecewise defined functions in LaTeX. These include:

• Using the cases environment to define the function.
• Using the & symbol to separate the function from the condition.
• Using the correct symbol for the condition (e.g., ≤ instead of <).
• Using a consistent formatting style throughout the document.

Common Applications of Piecewise Defined Functions

Piecewise defined functions have many applications in mathematics and science. Some common applications include:

• Modeling the behavior of electrical circuits.
• Modeling the motion of objects.
• Modeling the growth of populations.

Conclusion

In conclusion, piecewise defined functions are an important concept in mathematics and science. They are used to model real-world phenomena and have many applications. Writing piecewise defined functions in LaTeX is straightforward, but there are several common pitfalls to avoid. By following best practices and using the correct syntax, you can create professional-looking documents that contain mathematical equations and formulas.

Gallery of Piecewise Defined Functions in LaTeX

FAQs