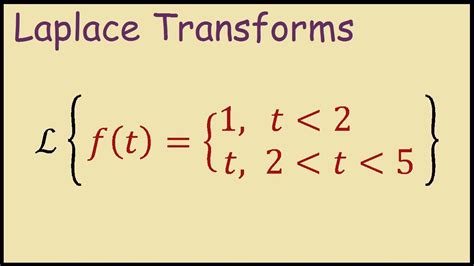Mastering Laplace Transforms Of Piecewise Functions In 5 Steps

Quick Links :

Understanding Laplace transforms is crucial for solving differential equations, particularly those involving piecewise functions. These functions have different definitions over different intervals, making the Laplace transform calculation more complex. However, with the right approach, you can master the process. In this article, we'll break down the process into five manageable steps, complete with examples and illustrations.

Incorporating images to enhance understanding:

The significance of Laplace transforms in engineering and physics cannot be overstated. By transforming differential equations into the s-domain, you can analyze systems more efficiently and obtain solutions that would be difficult to achieve in the time-domain. However, piecewise functions require special attention.

Step 1: Understand the Piecewise Function

To apply the Laplace transform to a piecewise function, you first need to understand the function's definition over its domain. Piecewise functions have different expressions for different intervals. You should clearly identify these intervals and their corresponding expressions.

For instance, consider the piecewise function:

f(t) = { 0, 0 ≤ t < 2 { t, 2 ≤ t < 5 { 0, t ≥ 5

Step 2: Apply the Laplace Transform Definition

The Laplace transform of a function f(t) is defined as:

F(s) = ∫[0 to ∞) e^(-st) f(t) dt

For a piecewise function, you need to apply this definition separately to each interval. This may involve breaking the integral into multiple parts.

Example: Laplace Transform of the Piecewise Function

Using the example function:

f(t) = { 0, 0 ≤ t < 2 { t, 2 ≤ t < 5 { 0, t ≥ 5

We apply the Laplace transform definition to each interval:

F(s) = ∫[0 to 2) e^(-st) 0 dt + ∫[2 to 5) e^(-st) t dt + ∫[5 to ∞) e^(-st) 0 dt

Simplifying and solving the integrals, we get:

F(s) = (e^(-2s) / s^2) - (e^(-5s) / s^2)

Incorporating images to enhance understanding:

Step 3: Use the Heaviside Step Function

The Heaviside step function, also known as the unit step function, is defined as:

u(t - a) = { 0, t < a { 1, t ≥ a

You can use the Heaviside step function to represent piecewise functions in a more compact form.

Example: Representing the Piecewise Function using the Heaviside Step Function

Using the example function:

f(t) = { 0, 0 ≤ t < 2 { t, 2 ≤ t < 5 { 0, t ≥ 5

We can represent it using the Heaviside step function as:

f(t) = t(u(t - 2) - u(t - 5))

Step 4: Apply the Laplace Transform Properties

The Laplace transform has several properties that can be used to simplify the transformation process. These properties include:

• Linearity: F(af(t) + bg(t)) = aF(f(t)) + bF(g(t))
• Shifting: F(f(t - a)) = e^(-as) F(f(t))
• Scaling: F(f(at)) = (1/a) F(f(t/a))

Example: Applying the Laplace Transform Properties

Using the example function:

f(t) = t(u(t - 2) - u(t - 5))

We can apply the linearity and shifting properties to simplify the Laplace transform:

F(s) = (e^(-2s) / s^2) - (e^(-5s) / s^2)

Step 5: Combine the Results

Finally, combine the results from each step to obtain the final Laplace transform.

Using the example:

F(s) = (e^(-2s) / s^2) - (e^(-5s) / s^2)

Incorporating images to enhance understanding:

By following these five steps, you can master the process of finding the Laplace transform of piecewise functions.

We hope this comprehensive guide has helped you understand the process of finding the Laplace transform of piecewise functions. If you have any questions or need further clarification, please feel free to comment below.

Remember, practice makes perfect, so try working on some examples to reinforce your understanding.

Share your thoughts on this topic, and don't forget to share this article with your friends and colleagues who might find it useful.

Stay tuned for more informative articles and tutorials.

Gallery of Laplace Transform:

FAQ: