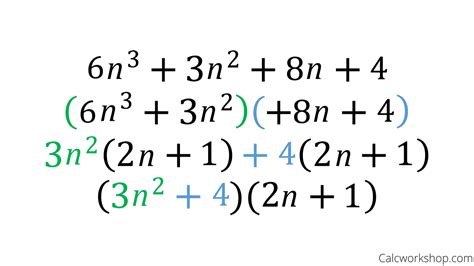Factoring trinomials by grouping is a powerful technique used to simplify complex algebraic expressions. It's a fundamental concept in mathematics, and mastering it can make a significant difference in solving equations and problems. In this article, we'll delve into the world of factoring trinomials by grouping, exploring its importance, benefits, and step-by-step instructions on how to do it.
What is Factoring Trinomials by Grouping?
Factoring trinomials by grouping is a method used to factorize quadratic expressions of the form ax^2 + bx + c, where a, b, and c are constants. This technique involves dividing the trinomial into two groups, factoring each group, and then combining the results.

Why is Factoring Trinomials by Grouping Important?
Factoring trinomials by grouping is an essential skill in algebra and mathematics. It helps in:
- Simplifying complex expressions
- Solving quadratic equations
- Finding the roots of quadratic equations
- Graphing quadratic functions
- Modeling real-world problems
Benefits of Factoring Trinomials by Grouping
Factoring trinomials by grouping has several benefits:
- Improved problem-solving skills: Mastering this technique can help you solve a wide range of problems in algebra and mathematics.
- Enhanced understanding of quadratic expressions: By factoring trinomials by grouping, you'll gain a deeper understanding of quadratic expressions and their properties.
- Increased confidence: Factoring trinomials by grouping can boost your confidence in solving algebraic problems.

Step-by-Step Instructions on Factoring Trinomials by Grouping
Factoring trinomials by grouping involves the following steps:
- Check if the trinomial is factorable: Make sure the trinomial is of the form ax^2 + bx + c and that it's factorable.
- Divide the trinomial into two groups: Divide the trinomial into two groups of two terms each.
- Factor each group: Factor each group separately using the distributive property.
- Combine the results: Combine the results of the two groups to get the final factored form.

Examples of Factoring Trinomials by Grouping
Let's consider a few examples to illustrate the technique:
- Example 1: Factor x^2 + 5x + 6
- Divide the trinomial into two groups: x^2 + 5x and 6
- Factor each group: x(x + 5) and 2 * 3
- Combine the results: x(x + 5) + 2 * 3 = (x + 3)(x + 2)
- Example 2: Factor x^2 + 7x + 12
- Divide the trinomial into two groups: x^2 + 7x and 12
- Factor each group: x(x + 7) and 3 * 4
- Combine the results: x(x + 7) + 3 * 4 = (x + 4)(x + 3)

Common Mistakes to Avoid When Factoring Trinomials by Grouping
When factoring trinomials by grouping, it's essential to avoid the following common mistakes:
- Incorrect grouping: Make sure to divide the trinomial into two groups of two terms each.
- Incorrect factoring: Factor each group correctly using the distributive property.
- Incorrect combination: Combine the results of the two groups correctly to get the final factored form.

Conclusion
Factoring trinomials by grouping is a powerful technique used to simplify complex algebraic expressions. By mastering this technique, you'll improve your problem-solving skills, enhance your understanding of quadratic expressions, and increase your confidence in solving algebraic problems. Remember to avoid common mistakes and practice regularly to become proficient in factoring trinomials by grouping.

Gallery of Factoring Trinomials by Grouping






What is factoring trinomials by grouping?
+Factoring trinomials by grouping is a method used to factorize quadratic expressions of the form ax^2 + bx + c.
Why is factoring trinomials by grouping important?
+Factoring trinomials by grouping is essential in algebra and mathematics, as it helps in simplifying complex expressions, solving quadratic equations, and finding the roots of quadratic equations.
What are the common mistakes to avoid when factoring trinomials by grouping?
+The common mistakes to avoid include incorrect grouping, incorrect factoring, and incorrect combination of the results.