5 Ways To Calculate Beta Weights From Anova

Quick Links :

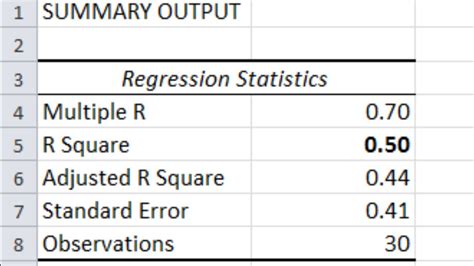
When analyzing the relationship between a dependent variable and one or more independent variables, statistical techniques like ANOVA (Analysis of Variance) are widely used. ANOVA helps in determining whether there are any statistically significant differences between the means of two or more groups. However, in scenarios where the researcher wants to understand the impact of multiple independent variables on a continuous dependent variable, techniques like regression analysis come into play. One critical component of regression analysis is the calculation of beta weights, which are also known as beta coefficients or standardized coefficients. These coefficients provide a way to compare the relative strength of the association between each independent variable and the dependent variable, after controlling for all other independent variables in the model.

In the context of ANOVA, which primarily deals with categorical independent variables, calculating beta weights directly is not feasible due to the nature of ANOVA. However, when transitioning from ANOVA to regression analysis, or when considering the effects of categorical variables in a regression framework, understanding how to derive or interpret coefficients in a way analogous to beta weights can be insightful. Here are five ways to approach the calculation or conceptual understanding of beta weights in the context of transitioning from ANOVA to more complex regression models:

1. Standardized Regression Coefficients

The most direct way to calculate beta weights is through multiple linear regression, where each independent variable's coefficient is standardized by dividing it by the standard deviation of the independent variable and then multiplying by the standard deviation of the dependent variable. This process ensures that the coefficients are on the same scale, allowing for direct comparison of the strength of the relationship between each independent variable and the dependent variable.

[ \text{Beta Weight} = \beta \times \frac{\sigma_{\text{predictor}}}{\sigma_{\text{outcome}}} ]

This method, however, is applied directly in regression analysis rather than ANOVA.

2. Dummy Coding for Categorical Variables

In scenarios where ANOVA is used with categorical independent variables, one can transition to a regression model by dummy coding these categorical variables. This involves creating binary variables for each category of the independent variable (except one, which serves as the reference category). By analyzing these dummy-coded variables in a regression model, one can interpret the coefficients as analogous to beta weights, understanding the impact of each category relative to the reference category.

3. Effect Size Measures

Effect size measures like Cohen's f or partial eta squared (η²) can provide insights into the strength of the association between independent variables and the dependent variable in ANOVA. While not directly calculating beta weights, these measures give a standardized way to evaluate the relative importance of each independent variable, akin to the concept of beta weights in regression.

4. Generalized Linear Models (GLMs)

GLMs extend traditional linear regression and ANOVA by allowing the response variable to have error distribution other than the normal distribution. For categorical independent variables, GLMs can be seen as a bridge between ANOVA and regression, offering a way to model and understand the effects of these variables in a more nuanced manner than traditional ANOVA, though not directly providing beta weights.

5. Bayesian Methods

Bayesian methods offer a flexible approach to modeling complex relationships between variables. By specifying prior distributions for model parameters (including those analogous to beta weights), Bayesian models can provide posterior distributions for these parameters, offering a probabilistic interpretation of their values. This approach allows for the incorporation of prior knowledge and the estimation of complex models that might not be feasible through traditional frequentist methods.

In conclusion, while ANOVA does not directly provide beta weights like regression analysis, understanding the principles of beta weights can help in interpreting the results of ANOVA and in transitioning to more complex regression models. The five methods described above offer different pathways for calculating, interpreting, or conceptualizing beta weights in the context of moving beyond traditional ANOVA.

Gallery of Transitioning from ANOVA to Regression

FAQ Section

Feel free to comment or ask questions about transitioning from ANOVA to regression analysis and interpreting beta weights.